

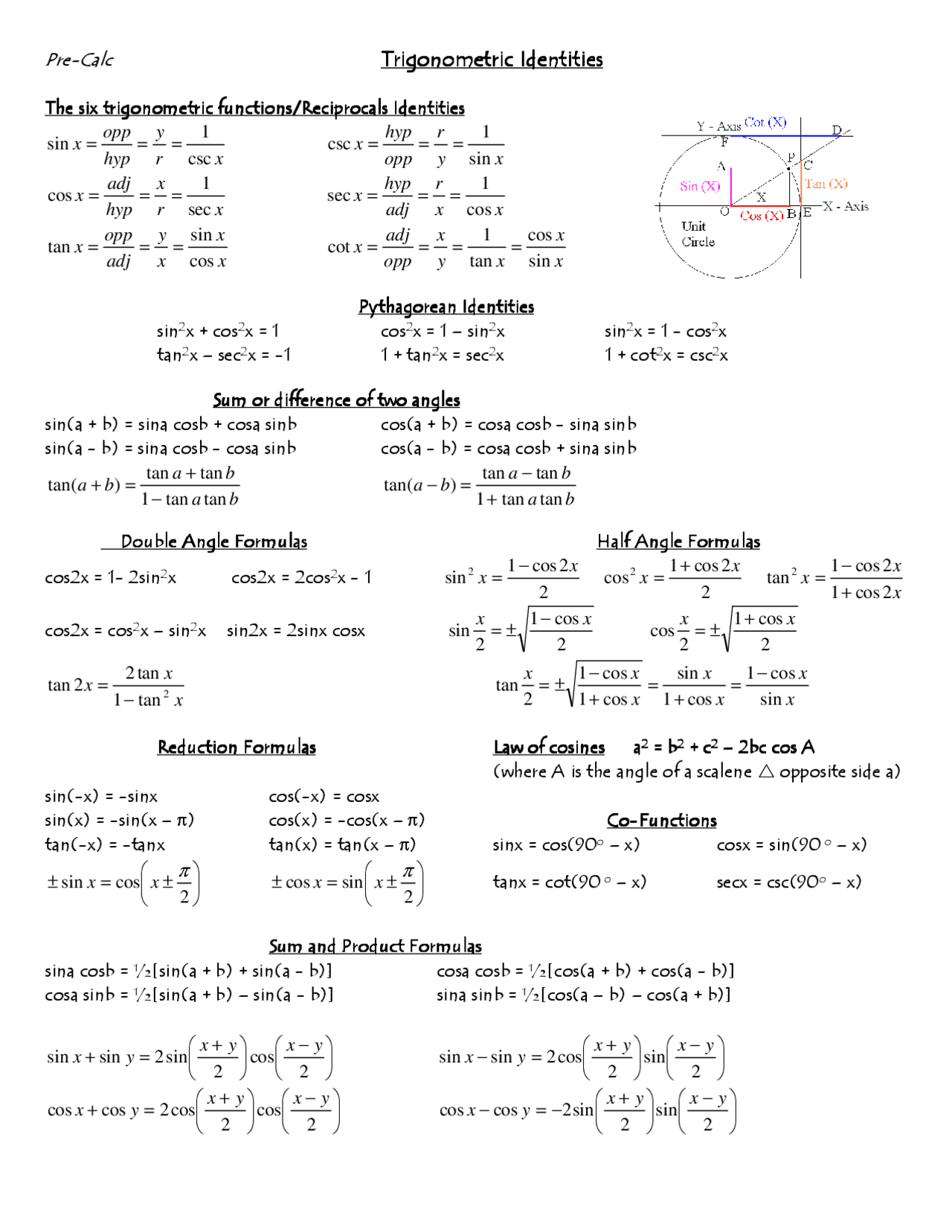
Keep it handy while you’re revising the concept, especially before an exam. This one page PDF covers summarised theory and the most important formulas related to the concept. Cheat sheets on Graph Transformations ( Basic and Advanced) are also available on this website. You also must have a strong grasp on graph transformations, which will help you to understand the relation between the graphs of trigonometric functions and inverse trionometric functions. A cheat sheet on Trigonometry is also available on this website. Use these to find (a) any trig function, given two known functions or (b) a 15pi function that isnt on the 16-point unit circle.
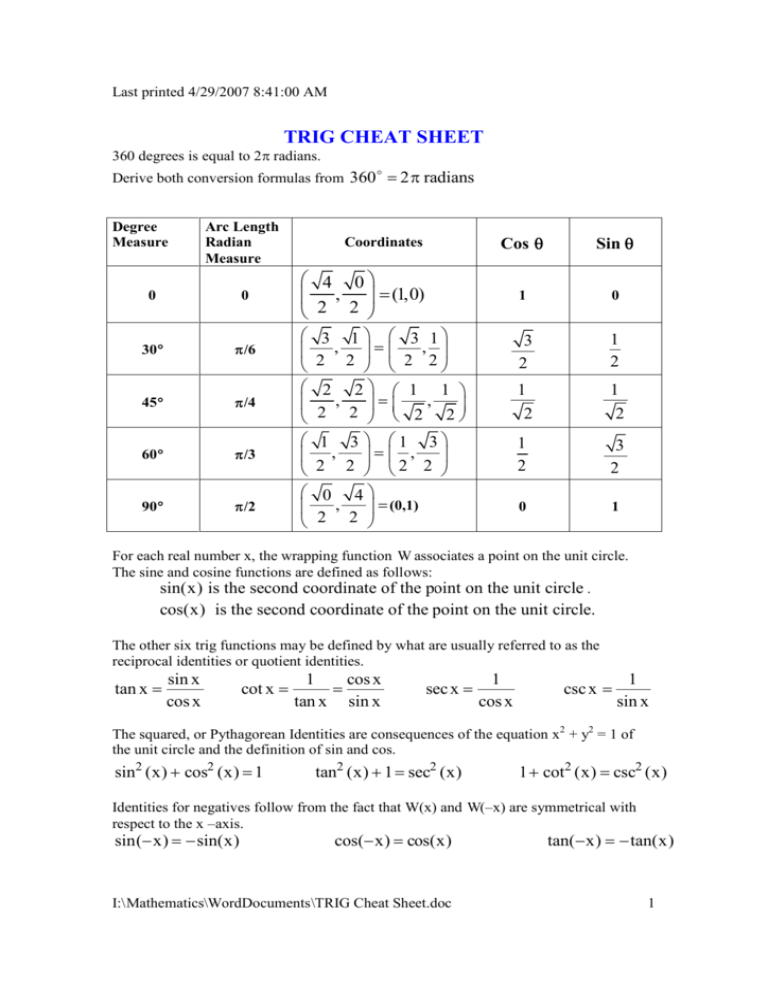
A study of these functions gives a good insight into the behaviour, domains and ranges of inverse functions in general.Ī good knowledge of the basic formulae of trigonometry is a must to understand and solve problems related to inverse trigonometry. This topic is a part of trigonometry and is an intersection of two major concepts – inverse of a function and trigonometry. Substituting x with ix in these two formulas and keeping in mind that i 2 = −1 it's immediate to deduce that cosh x = cos (ix) and sinh x = −i sin (ix) (I mention this just for the sake of completeness and because it's fun!).This cheat sheet covers the high school math concept – Inverse Trigonometric Functions. 2 Definitions Definition of hyperbolic sine and cosine: sinh x = e x − e −x 2 cosh x = e x + e −x 2 There are two equivalent formulas for sine and cosine (Euler's formulas) but they require some knowledge of the complex numbers: sin x = e ix − e −ix 2i cos x = e ix + e −ix 2 where i = √ −1 or if you prefer i 2 = −1. The main purpose of this paper is not to give you a bunch of formulas to memorize, but to make you aware of the fact that hyperbolic formulas are just like trig formulas up to signs and correct signs can always be checked with some very quick calculation. For each formula I will explicitly state if some change of sign occurs or not (the different sign is marked in green). Most of the formulas that follow correspond precisely to a trig formula or they differ by at most a change of sign. For the moment we have to postpone this discussion to the end of Calc3 or Calc4, but still we should be aware of the fact that the impressive similarity between trig formulas and hyperbolic formulas is not a pure coincidence. Roughly speaking ordinary trigonometric functions are trigonometric functions of purely real numbers, and hyperbolic functions are trigonometric functions of purely imaginary numbers. Unfortunately this can be completely understood only if you have some knowledge of the complex numbers. For historical reasons hyperbolic functions have little or no room at all in the syllabus of a calculus course, but as a matter of fact they have the same dignity as trigonometric functions.


 0 kommentar(er)
0 kommentar(er)
